MATHS WONDERLAND: Formulae

PMR

INTERNATIONAL MATHEMATICS SYMBOLS

Symbol in HTML	Symbol in $T E X$	Name	Explanation	Examples
		Read as
		Category
=	$= \!\,$	equality is equal to; equals everywhere	x = y means x and y represent the same thing or value.	2 = 2 1 + 1 = 2
≠	$\ne \!\,$	inequality is not equal to; does not equal everywhere	x ≠ y means that x and y do not represent the same thing or value. (The forms !=, /= or <> are generally used in programming languages where ease of typing and use of ASCII text is preferred.)	2 + 2 ≠ 5
< >	$< \!\,$ $> \!\,$	strict inequality is less than, is greater than order theory	x < y means x is less than y. x > y means x is greater than y.	3 < 4 5 > 4
< >	$< \!\,$ $> \!\,$	proper subgroup is a proper subgroup of group theory	H < G means H is a proper subgroup of G.	5Z < Z A₃ < S₃

				x ≪ e^x
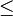≤ ≥	$\le \!\,$ $\ge \!\,$	inequality is less than or equal to, is greater than or equal to order theory	x ≤ y means x is less than or equal to y. x ≥ y means x is greater than or equal to y. (The forms <= and >= are generally used in programming languages where ease of typing and use of ASCII text is preferred.)	3 ≤ 4 and 5 ≤ 5 5 ≥ 4 and 5 ≥ 5
		subgroup is a subgroup of group theory	H ≤ G means H is a subgroup of G.	Z ≤ Z A₃ ≤ S₃
		reduction is reducible to computational complexity theory	A ≤ B means the problem A can be reduced to the problem B. Subscripts can be added to the ≤ to indicate what kind of reduction.	If $\exists f \in F \mbox{ . } \forall x \in \mathbb{N} \mbox{ . } x \in A \Leftrightarrow f(x) \in B$ then $A \leq_{F} B$
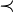≺	$\prec \!\,$	Karp reduction is Karp reducible to; is polynomial-time many-one reducible to computational complexity theory	L₁ ≺ L₂ means that the problem L₁ is Karp reducible to L₂.^[1]	If L₁ ≺ L₂ and L₂ ∈ P, then L₁ ∈ P.
∝	$\propto \!\,$	proportionality is proportional to; varies as everywhere	y ∝ x means that y = kx for some constant k.	if y = 2x, then y ∝ x.
∝	$\propto \!\,$	Karp reduction^[2] is Karp reducible to; is polynomial-time many-one reducible to computational complexity theory	A ∝ B means the problem A can be polynomially reduced to the problem B.	If L₁ ∝ L₂ and L₂ ∈ P, then L₁ ∈ P.
+	$+ \!\,$	addition plus; add arithmetic	4 + 6 means the sum of 4 and 6.	2 + 7 = 9
+	$+ \!\,$	disjoint union the disjoint union of ... and ... set theory	A₁ + A₂ means the disjoint union of sets A₁ and A₂.	A₁ = {3, 4, 5, 6} ∧ A₂ = {7, 8, 9, 10} ⇒ A₁ + A₂ = {(3,1), (4,1), (5,1), (6,1), (7,2), (8,2), (9,2), (10,2)}
−	$- \!\,$	subtraction minus; take; subtract arithmetic	9 − 4 means the subtraction of 4 from 9.	8 − 3 = 5
		negative sign negative; minus; the opposite of arithmetic	−3 means the negative of the number 3.	−(−5) = 5
		set-theoretic complement minus; without set theory	A − B means the set that contains all the elements of A that are not in B. (∖ can also be used for set-theoretic complement as described below.)	{1,2,4} − {1,3,4} = {2}
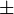±	$\pm \!\,$	plus-minus plus or minus arithmetic	6 ± 3 means both 6 + 3 and 6 − 3.	The equation x = 5 ± √4, has two solutions, x = 7 and x = 3.
±	$\pm \!\,$	plus-minus plus or minus measurement	10 ± 2 or equivalently 10 ± 20% means the range from 10 − 2 to 10 + 2.	If a = 100 ± 1 mm, then a ≥ 99 mm and a ≤ 101 mm.
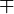∓	$\mp \!\,$	minus-plus minus or plus arithmetic	6 ± (3 ∓ 5) means both 6 + (3 − 5) and 6 − (3 + 5).	cos(x ± y) = cos(x) cos(y) ∓ sin(x) sin(y).
×	$\times \!\,$	multiplication times; multiplied by arithmetic	3 × 4 means the multiplication of 3 by 4. (The symbol * is generally used in programming languages, where ease of typing and use of ASCII text is preferred.)	7 × 8 = 56
		Cartesian product the Cartesian product of ... and ...; the direct product of ... and ... set theory	X×Y means the set of all ordered pairs with the first element of each pair selected from X and the second element selected from Y.	{1,2} × {3,4} = {(1,3),(1,4),(2,3),(2,4)}
		cross product cross linear algebra	u × v means the cross product of vectors u and v	(1,2,5) × (3,4,−1) = (−22, 16, − 2)
		group of units the group of units of ring theory	R^× consists of the set of units of the ring R, along with the operation of multiplication. This may also be written R* as described below, or U(R).	$\begin{align} (\mathbb{Z} / 5\mathbb{Z})^\times & = \{ [1], [2], [3], [4] \} \\ & \cong C_4 \\ \end{align}$
*	$* \!\,$	multiplication times; multiplied by arithmetic	a * b means the product of a and b. (Multiplication can also be denoted with × or ⋅, or even simple juxtaposition. * is generally used where ease of typing and use of ASCII text is preferred, such as programming languages.)	4 * 3 means the product of 4 and 3, or 12.
		convolution convolution; convolved with functional analysis	f * g means the convolution of f and g.	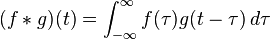$(f * g)(t) = \int_{-\infty}^{\infty} f(\tau) g(t - \tau)\, d\tau$ .
		complex conjugate conjugate complex numbers	z* means the complex conjugate of z. ( $\bar{z}$ can also be used for the conjugate of z, as described below.)	$(3+4i)^\ast = 3-4i$ .
		group of units the group of units of ring theory	R* consists of the set of units of the ring R, along with the operation of multiplication. This may also be written R^× as described above, or U(R).	$\begin{align} (\mathbb{Z} / 5\mathbb{Z})^\ast & = \{ [1], [2], [3], [4] \} \\ & \cong C_4 \\ \end{align}$
		hyperreal numbers the (set of) hyperreals non-standard analysis	*R means the set of hyperreal numbers. Other sets can be used in place of R.	*N is the hypernatural numbers.
		Hodge dual Hodge dual; Hodge star linear algebra	v means the Hodge dual of a vector v. If v is a k-vector within an n-dimensional oriented inner product space, then v is an (n−k)-vector.	If ${e i}$ are the standard basis vectors of 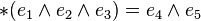$\mathbb{R}^5$ , $*(e_1\wedge e_2\wedge e_3)= e_4\wedge e_5$
·	$\cdot \!\,$	multiplication times; multiplied by arithmetic	3 · 4 means the multiplication of 3 by 4.	7 · 8 = 56
		dot product dot linear algebra	u · v means the dot product of vectors u and v	(1,2,5) · (3,4,−1) = 6
		placeholder (silent) functional analysis	A · means a placeholder for an argument of a function. Indicates the functional nature of an expression without assigning a specific symbol for an argument.	$\\|\cdot\\|$
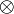⊗	$\otimes \!\,$	tensor product, tensor product of modules tensor product of linear algebra	$V \otimes U$ means the tensor product of V and U.^[3] $V \otimes_R U$ means the tensor product of modules V and U over the ring R.	{1, 2, 3, 4} ⊗ {1, 1, 2} = {{1, 2, 3, 4}, {1, 2, 3, 4}, {2, 4, 6, 8}}
÷ ⁄	$\div \!\,$ $/ \!\,$	division (Obelus) divided by; over arithmetic	6 ÷ 3 or 6 ⁄ 3 means the division of 6 by 3.	2 ÷ 4 = 0.5 12 ⁄ 4 = 3
		quotient group mod group theory	G / H means the quotient of group G modulo its subgroup H.	{0, a, 2a, b, b+a, b+2a} / {0, b} = {{0, b}, {a, b+a}, {2a, b+2a}}
		quotient set mod set theory	A/~ means the set of all ~ equivalence classes in A.	If we define ~ by x ~ y ⇔ x − y ∈ ℤ, then ℝ/~ = { {x + n : n ∈ ℤ } : x ∈ [0,1) }
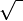√	$\surd \!\,$ $\sqrt{\ } \!\,$	square root the (principal) square root of real numbers	$\sqrt{x}$ means the nonnegative number whose square is $x$ .	$\sqrt{4}=2$
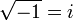√	$\surd \!\,$ $\sqrt{\ } \!\,$	complex square root the (complex) square root of complex numbers	if $z=r\,\exp(i\phi)$ is represented in polar coordinates with $-\pi < \phi \le \pi$ , then $\sqrt{z} = \sqrt{r} \exp(i \phi/2)$ .	$\sqrt{-1}=i$
x	$\bar{x} \!\,$	mean overbar; … bar statistics	$\bar{x}$ (often read as “x bar”) is the mean (average value of $x i$ ).	$x = \{1,2,3,4,5\}; \bar{x} = 3$ .
		complex conjugate conjugate complex numbers	$\overline{z}$ means the complex conjugate of z. (z* can also be used for the conjugate of z, as described above.)	$\overline{3+4i} = 3-4i$ .
		algebraic closure algebraic closure of field theory	$\overline{F}$ is the algebraic closure of the field F.	The field of algebraic numbers is sometimes denoted as $\overline{\mathbb{Q}}$ because it is the algebraic closure of the rational numbers ${\mathbb{Q}}$ .
		topological closure (topological) closure of topology	$\overline{S}$ is the topological closure of the set S. This may also be denoted as cl(S) or Cl(S).	In the space of the real numbers, $\overline{\mathbb{Q}} = \mathbb{R}$ (the rational numbers are dense in the real numbers).
\|…\|	$\| \ldots \| \!\,$	absolute value; modulus absolute value of; modulus of numbers	\|x\| means the distance along the real line (or across the complex plane) between xand zero.	\|3\| = 3 \|–5\| = \|5\| = 5 \| i \| = 1 \| 3 + 4i \| = 5
		Euclidean norm or Euclidean length or magnitude Euclidean norm of geometry	\|x\| means the (Euclidean) length of vector x.	For x = (3,-4) $\|\textbf{x}\| = \sqrt{3^2 + (-4)^2} = 5$
		determinant determinant of matrix theory	\|A\| means the determinant of the matrix A	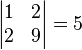$\begin{vmatrix} 1&2 \\ 2&9 \\ \end{vmatrix} = 5$
		cardinality cardinality of; size of; order of set theory	\|X\| means the cardinality of the set X. (# may be used instead as described below.)	\|{3, 5, 7, 9}\| = 4.
\|\|…\|\|	$\\| \ldots \\| \!\,$	norm norm of; length of linear algebra	\|\| x \|\| means the norm of the element x of a normed vector space.^[4]	\|\| x + y \|\| ≤ \|\| x \|\| + \|\| y \|\|
\|\|…\|\|	$\\| \ldots \\| \!\,$	nearest integer function nearest integer to numbers	\|\|x\|\| means the nearest integer to x. (This may also be written [x], ⌊x⌉, nint(x) or Round(x).)	\|\|1\|\| = 1, \|\|1.6\|\| = 2, \|\|−2.4\|\| = −2, \|\|3.49\|\| = 3
∣ ∤	$\mid \!\,$ $\nmid \!\,$	divisor, divides divides number theory	a\|b means a divides b. a∤b means a does not divide b. (This symbol can be difficult to type, and its negation is rare, so a regular but slightly shorter vertical bar \| character can be used.)	Since 15 = 3×5, it is true that 3\|15 and 5\|15.
		conditional probability given probability	P(A\|B) means the probability of the event a occurring given that b occurs.	if X is a uniformly random day of the year P(X is May 25 \| X is in May) = 1/31
		restriction restriction of … to …; restricted to set theory	f\|_A means the function f restricted to the set A, that is, it is the function withdomain A ∩ dom(f) that agrees with f.	The function f : R → R defined by f(x) = x² is not injective, but f\|_R⁺is injective.
		such that such that; so that everywhere	\| means “such that”, see ":" (described below).	S = {(x,y) \| 0 < y < f(x)} The set of (x,y) such that y is greater than 0 and less than f(x).
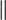\|\|	$\\| \!\,$	parallel is parallel to geometry	x \|\| y means x is parallel to y.	If l \|\| m and m ⊥ n then l ⊥ n.
		incomparability is incomparable to order theory	x \|\| y means x is incomparable to y.	{1,2} \|\| {2,3} under set containment.
		exact divisibility exactly divides number theory	p^a \|\| n means p^a exactly divides n (i.e. p^a divides n but p^a+1 does not).	2³ \|\| 360.
#	$\# \!\,$	cardinality cardinality of; size of; order of set theory	#X means the cardinality of the set X. (\|…\| may be used instead as described above.)	#{4, 6, 8} = 3
#	$\# \!\,$	connected sum connected sum of; knot sum of; knot composition of topology, knot theory	A#B is the connected sum of the manifolds A and B. If A and B are knots, then this denotes the knot sum, which has a slightly stronger condition.	A#S^m is homeomorphic to A, for any manifold A, and the sphereS^m.
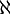ℵ	$\aleph \!\,$	aleph number aleph set theory	ℵ_α represents an infinite cardinality (specifically, the α-th one, where α is an ordinal).	\|ℕ\| = ℵ₀, which is called aleph-null.
ℶ	$\beth \!\,$	beth number beth set theory	ℶ_α represents an infinite cardinality (similar to ℵ, but ℶ does not necessarily index all of the numbers indexed by ℵ. ).	$\beth_1 = \|P(\mathbb{N})\| = 2^{\aleph_0}.$
𝔠	$\mathfrak c \!\,$	cardinality of the continuum cardinality of the continuum; c; cardinality of the real numbers set theory	The cardinality of $\mathbb R$ is denoted by $\|\mathbb R\|$ or by the symbol $\mathfrak c$ (a lowercase Frakturletter C).	$\mathfrak c = {\beth}_{1}$
:	$: \!\,$	such that such that; so that everywhere	: means “such that”, and is used in proofs and the set-builder notation (described below).	∃ n ∈ ℕ: n is even.
		field extension extends; over field theory	K : F means the field K extends the field F. This may also be written as K ≥ F.	ℝ : ℚ
		inner product of matrices inner product of linear algebra	A : B means the Frobenius inner product of the matrices A and B. The general inner product is denoted by ⟨u, v⟩, ⟨u \| v⟩ or (u \| v), as described below. For spatial vectors, the dot product notation, x·y is common. See also Bra-ket notation.	$A:B = \sum_{i,j} A_{ij}B_{ij}\!\,$
		index of a subgroup index of subgroup group theory	The index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" (cosets) of H that fill up G	$\|G:H\| = \frac{\|G\|}{\|H\|}$
!	$! \!\,$	factorial factorial combinatorics	n! means the product 1 × 2 × ... × n.	4! = 1 × 2 × 3 × 4 = 24
!	$! \!\,$	logical negation not propositional logic	The statement !A is true if and only if A is false. A slash placed through another operator is the same as "!" placed in front. (The symbol ! is primarily from computer science. It is avoided in mathematical texts, where the notation ¬A is preferred.)	!(!A) ⇔ A x ≠ y ⇔ !(x = y)
~	$\sim \!\,$	probability distribution has distribution statistics	X ~ D, means the random variable X has the probability distribution D.	X ~ N(0,1), the standard normal distribution
		row equivalence is row equivalent to matrix theory	A~B means that B can be generated by using a series of elementary row operations on A	$\begin{bmatrix} 1&2 \\ 2&4 \\ \end{bmatrix} \sim \begin{bmatrix} 1&2 \\ 0&0 \\ \end{bmatrix}$
		same order of magnitude roughly similar; poorly approximates approximation theory	m ~ n means the quantities m and n have the same order of magnitude, or general size. (Note that ~ is used for an approximation that is poor, otherwise use ≈ .)	2 ~ 5 8 × 9 ~ 100 but π² ≈ 10
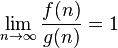		asymptotically equivalent is asymptotically equivalent to asymptotic analysis	f ~ g means $\lim_{n\to\infty} \frac{f(n)}{g(n)} = 1$ .	x ~ x+1
		equivalence relation are in the same equivalence class everywhere	a ~ b means $b \in [a]$ (and equivalently $a \in [b]$ ).	1 ~ 5 mod 4
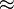≈	$\approx \!\,$	approximately equal is approximately equal to everywhere	x ≈ y means x is approximately equal to y. This may also be written ≃, ≅, ~ or ≒.	π ≈ 3.14159
≈	$\approx \!\,$	isomorphism is isomorphic to group theory	G ≈ H means that group G is isomorphic (structurally identical) to group H. (≅ can also be used for isomorphic, as described below.)	Q / {1, −1} ≈ V, where Q is the quaternion group and V is the Klein four-group.
≀	$\wr \!\,$	wreath product wreath product of … by … group theory	A ≀ H means the wreath product of the group A by the group H. This may also be written A_wr H.	$S_n \wr Z_2$ is isomorphic to the automorphism group of thecomplete bipartite graph on (n,n) vertices.
◅ ▻	$\triangleleft \!\,$ $\triangleright \!\,$	normal subgroup is a normal subgroup of group theory	N ◅ G means that N is a normal subgroup of group G.	Z(G) ◅ G
		ideal is an ideal of ring theory	I ◅ R means that I is an ideal of ring R.	(2) ◅ Z
		antijoin the antijoin of relational algebra	R ▻ S means the antijoin of the relations R and S, the tuples in R for which there is not a tuple in S that is equal on their common attribute names.	R $\triangleright$ S = R - R $\ltimes$ S
⋉ ⋊	$\ltimes \!\,$ $\rtimes \!\,$	semidirect product the semidirect product of group theory	N ⋊_φ H is the semidirect product of N (a normal subgroup) and H (a subgroup), with respect to φ. Also, if G = N ⋊_φ H, then G is said to split over N. (⋊ may also be written the other way round, as ⋉, or as ×.)	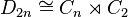$D_{2n} \cong C_n \rtimes C_2$
⋉ ⋊	$\ltimes \!\,$ $\rtimes \!\,$	semijoin the semijoin of relational algebra	R ⋉ S is the semijoin of the relations R and S, the set of all tuples in R for which there is a tuple in S that is equal on their common attribute names.	R 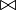$\ltimes$ S = $Π$ _{a₁,..,a_n}(R $\bowtie$ S)
⋈	$\bowtie \!\,$	natural join the natural join of relational algebra	R ⋈ S is the natural join of the relations R and S, the set of all combinations of tuples in R and S that are equal on their common attribute names.
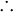∴	$\therefore \!\,$	therefore therefore; so; hence everywhere	Sometimes used in proofs before logical consequences.	All humans are mortal. Socrates is a human. ∴ Socrates is mortal.
∵	$\because \!\,$	because because; since everywhere	Sometimes used in proofs before reasoning.	3331 is prime ∵ it has no positive integer factors other than itself and one.
■ □ ∎ ▮ ‣	$\blacksquare \!\,$ $\Box \!\,$ $\blacktriangleright \!\,$	end of proof QED; tombstone; Halmos symbol everywhere	Used to mark the end of a proof. (May also be written Q.E.D.)
■ □ ∎ ▮ ‣		D'Alembertian non-Euclidean Laplacian vector calculus	It is the generalisation of the Laplace operator in the sense that it is the differential operator which is invariant under the isometry group of the underlying space and it reduces to the Laplace operator if restricted to time independent functions.	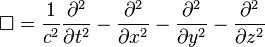$\square = \frac{1}{c^2}{\partial^2 \over \partial t^2 } - {\partial^2 \over \partial x^2 } - {\partial^2 \over \partial y^2 } - {\partial^2 \over \partial z^2 }$
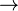⇒ → ⊃	$\Rightarrow \!\,$ $\rightarrow \!\,$ $\supset \!\,$	material implication implies; if … then propositional logic, Heyting algebra	A ⇒ B means if A is true then B is also true; if A is false then nothing is said about B. (→ may mean the same as ⇒, or it may have the meaning for functions given below.) (⊃ may mean the same as ⇒,^[5] or it may have the meaning for superset given below.)	x = 2 ⇒ x² = 4 is true, but x² = 4 ⇒ x = 2 is in general false (since x could be −2).
⇔ ↔	$\Leftrightarrow \!\,$ $\leftrightarrow \!\,$	material equivalence if and only if; iff propositional logic	A ⇔ B means A is true if B is true and A is false if B is false.	x + 5 = y + 2 ⇔ x + 3 = y
¬ ˜	$\neg \!\,$ $\sim \!\,$	logical negation not propositional logic	The statement ¬A is true if and only if A is false. A slash placed through another operator is the same as "¬" placed in front. (The symbol ~ has many other uses, so ¬ or the slash notation is preferred. Computer scientists will often use ! but this is avoided in mathematical texts.)	¬(¬A) ⇔ A x ≠ y ⇔ ¬(x = y)
∧	$\and \!\,$	logical conjunction or meetin a lattice and; min; meet propositional logic, lattice theory	The statement A ∧ B is true if A and B are both true; else it is false. For functions A(x) and B(x), A(x) ∧ B(x) is used to mean min(A(x), B(x)).	n < 4 ∧ n >2 ⇔ n = 3 when n is a natural number.
		wedge product wedge product; exterior product linear algebra	u ∧ v means the wedge product of vectors u and v. This generalizes the cross product to higher dimensions. (For vectors in R³, × can also be used.)	$u \wedge v = u \times v, \mbox{ if } u, v \in \mathbb{R}^3$
		exponentiation … (raised) to the power of … everywhere	a ^ b means a raised to the power of b (a ^ b is more commonly written a^b. The symbol ^ is generally used in programming languages where ease of typing and use of plain ASCII text is preferred.)	2^3 = 2³ = 8
∨	$\or \!\,$	logical disjunction or joinin a lattice or; max; join propositional logic, lattice theory	The statement A ∨ B is true if A or B (or both) are true; if both are false, the statement is false. For functions A(x) and B(x), A(x) ∨ B(x) is used to mean max(A(x), B(x)).	n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 when n is a natural number.
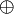⊕ ⊻	$\oplus \!\,$ $\veebar \!\,$	exclusive or xor propositional logic, Boolean algebra	The statement A ⊕ B is true when either A or B, but not both, are true. A ⊻ Bmeans the same.	(¬A) ⊕ A is always true, A ⊕ A is always false.
⊕ ⊻	$\oplus \!\,$ $\veebar \!\,$	direct sum direct sum of abstract algebra	The direct sum is a special way of combining several objects into one general object. (The bun symbol ⊕, or the coproduct symbol ∐, is used; ⊻ is only for logic.)	Most commonly, for vector spaces U, V, and W, the following consequence is used: U = V ⊕ W ⇔ (U = V + W) ∧ (V ∩ W = {0})
∀	$\forall \!\,$	universal quantification for all; for any; for each predicate logic	∀ x: P(x) means P(x) is true for all x.	∀ n ∈ ℕ: n² ≥ n.
∃	$\exists \!\,$	existential quantification there exists; there is; there are predicate logic	∃ x: P(x) means there is at least one x such that P(x) is true.	∃ n ∈ ℕ: n is even.
∃!	$\exists! \!\,$	uniqueness quantification there exists exactly one predicate logic	∃! x: P(x) means there is exactly one x such that P(x) is true.	∃! n ∈ ℕ: n + 5 = 2n.
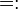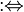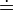=: := ≡ :⇔ ≜ ≝ ≐	$=: \!\,$ $:= \!\,$ $\equiv \!\,$ $:\Leftrightarrow \!\,$ $\triangleq \!\,$ $\overset{\underset{\mathrm{def}}{}}{=} \!\,$ $\doteq \!\,$	definition is defined as; is equal by definition to everywhere	x := y, y =: x or x ≡ y means x is defined to be another name for y, under certain assumptions taken in context. (Some writers use ≡ to mean congruence). P :⇔ Q means P is defined to be logically equivalent to Q.	$\cosh x := \frac{e^x + e^{-x}}{2}$
≅	$\cong \!\,$	congruence is congruent to geometry	△ABC ≅ △DEF means triangle ABC is congruent to (has the same measurements as) triangle DEF.
≅	$\cong \!\,$	isomorphic is isomorphic to abstract algebra	G ≅ H means that group G is isomorphic (structurally identical) to group H. (≈ can also be used for isomorphic, as described above.)	$\mathbb{R}^2 \cong \mathbb{C}$ .
≡	$\equiv \!\,$	congruence relation ... is congruent to ... modulo ... modular arithmetic	a ≡ b (mod n) means a − b is divisible by n	5 ≡ 2 (mod 3)
{ , }	${\{\ ,\!\ \}} \!\,$	set brackets the set of … set theory	{a,b,c} means the set consisting of a, b, and c.^[6]	ℕ = { 1, 2, 3, …}
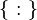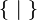{ : } { \| }	$\{\ :\ \} \!\,$ $\{\ \|\ \} \!\,$	set builder notation the set of … such that set theory	{x : P(x)} means the set of all x for which P(x) is true.^[6] {x \| P(x)} is the same as {x : P(x)}.	{n ∈ ℕ : n² < 20} = { 1, 2, 3, 4}
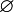∅ { }	$\empty \!\,$ $\varnothing \!\,$ $\{\} \!\,$	empty set the empty set set theory	∅ means the set with no elements.^[6] { } means the same.	{n ∈ ℕ : 1 < n² < 4} = ∅
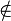∈ ∉	$\in \!\,$ $\notin \!\,$	set membership is an element of; is not an element of everywhere, set theory	a ∈ S means a is an element of the set S;^[6] a ∉ S means a is not an element ofS.^[6]	(1/2)⁻¹ ∈ ℕ 2⁻¹ ∉ ℕ
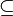⊆ ⊂	$\subseteq \!\,$ $\subset \!\,$	subset is a subset of set theory	(subset) A ⊆ B means every element of A is also an element of B.^[7] (proper subset) A ⊂ B means A ⊆ B but A ≠ B. (Some writers use the symbol ⊂ as if it were the same as ⊆.)	(A ∩ B) ⊆ A ℕ ⊂ ℚ ℚ ⊂ ℝ
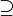⊇ ⊃	$\supseteq \!\,$ $\supset \!\,$	superset is a superset of set theory	A ⊇ B means every element of B is also an element of A. A ⊃ B means A ⊇ B but A ≠ B. (Some writers use the symbol ⊃ as if it were the same as ⊇.)	(A ∪ B) ⊇ B ℝ ⊃ ℚ
∪	$\cup \!\,$	set-theoretic union the union of … or …; union set theory	A ∪ B means the set of those elements which are either in A, or in B, or in both.^[7]	A ⊆ B ⇔ (A ∪ B) = B
∩	$\cap \!\,$	set-theoretic intersection intersected with; intersect set theory	A ∩ B means the set that contains all those elements that A and B have in common.^[7]	{x ∈ ℝ : x² = 1} ∩ ℕ = {1}
∆	$\vartriangle \!\,$	symmetric difference symmetric difference set theory	A ∆ B means the set of elements in exactly one of A or B. (Not to be confused with delta, Δ, described below.)	{1,5,6,8} ∆ {2,5,8} = {1,2,6}
∖	$\setminus \!\,$	set-theoretic complement minus; without set theory	A ∖ B means the set that contains all those elements of A that are not in B.^[7] (− can also be used for set-theoretic complement as described above.)	{1,2,3,4} ∖ {3,4,5,6} = {1,2}
→	$\to \!\,$	function arrow from … to set theory, type theory	f: X → Y means the function f maps the set X into the set Y.	Let f: ℤ → ℕ∪{0} be defined by f(x) := x².
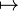↦	$\mapsto \!\,$	function arrow maps to set theory	f: a ↦ b means the function f maps the element a to the element b.	Let f: x ↦ x+1 (the successor function).
∘	$\circ \!\,$	function composition composed with set theory	f∘g is the function, such that (f∘g)(x) = f(g(x)).^[8]	if f(x) := 2x, and g(x) := x + 3, then (f∘g)(x) = 2(x + 3).
ℕ N	$\mathbb{N} \!\,$ $\mathbf{N} \!\,$	natural numbers N; the (set of) natural numbers numbers	N means either { 0, 1, 2, 3, ...} or { 1, 2, 3, ...}. The choice depends on the area of mathematics being studied; e.g. number theorists prefer the latter; analysts, set theorists and computer scientists prefer the former. To avoid confusion, always check an author's definition of N. Set theorists often use the notation ω (for least infinite ordinal) to denote the set of natural numbers (including zero), along with the standard ordering relation ≤.	ℕ = {\|a\| : a ∈ ℤ} or ℕ = {\|a\| > 0: a ∈ ℤ}
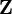ℤ Z	$\mathbb{Z} \!\,$ $\mathbf{Z} \!\,$	integers Z; the (set of) integers numbers	ℤ means {..., −3, −2, −1, 0, 1, 2, 3, ...}. ℤ⁺ or ℤ^> means {1, 2, 3, ...} . ℤ^* or ℤ^≥ means {0, 1, 2, 3, ...} .	ℤ = {p, −p : p ∈ ℕ ∪ {0}}
ℤ_n ℤ_p Z_n Z_p	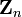$\mathbb{Z}_n \!\,$ $\mathbb{Z}_p \!\,$ $\mathbf{Z}_n \!\,$ $\mathbf{Z}_p \!\,$	integers mod n Z_n; the (set of) integers modulon numbers	ℤ_n means {[0], [1], [2], ...[n−1]} with addition and multiplication modulo n. Note that any letter may be used instead of n, such as p. To avoid confusion with p-adic numbers, use ℤ/pℤ or ℤ/(p) instead.	ℤ₃ = {[0], [1], [2]}
ℤ_n ℤ_p Z_n Z_p		p-adic integers the (set of) p-adic integers numbers	Note that any letter may be used instead of p, such as n or l.
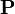ℙ P	$\mathbb{P} \!\,$ $\mathbf{P} \!\,$	projective space P; the projective space; the projective line; the projective plane topology	ℙ means a space with a point at infinity.	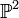$\mathbb{P}^1$ , $\mathbb{P}^2$
ℙ P	$\mathbb{P} \!\,$ $\mathbf{P} \!\,$	probability the probability of probability theory	ℙ(X) means the probability of the event X occurring. This may also be written as P(X), Pr(X), P[X] or Pr[X].	If a fair coin is flipped, ℙ(Heads) = ℙ(Tails) = 0.5.
ℚ Q	$\mathbb{Q} \!\,$ $\mathbf{Q} \!\,$	rational numbers Q; the (set of) rational numbers; the rationals numbers	ℚ means {p/q : p ∈ ℤ, q ∈ ℕ}.	3.14000... ∈ ℚ π ∉ ℚ
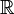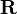ℝ R	$\mathbb{R} \!\,$ $\mathbf{R} \!\,$	real numbers R; the (set of) real numbers; the reals numbers	ℝ means the set of real numbers.	π ∈ ℝ √(−1) ∉ ℝ
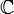ℂ C	$\mathbb{C} \!\,$ $\mathbf{C} \!\,$	complex numbers C; the (set of) complex numbers numbers	ℂ means {a + b i : a,b ∈ ℝ}.	i = √(−1) ∈ ℂ
ℍ H	$\mathbb{H} \!\,$ $\mathbf{H} \!\,$	quaternions or Hamiltonian quaternions H; the (set of) quaternions numbers	ℍ means {a + b i + c j + d k : a,b,c,d ∈ ℝ}.
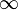O	$O$	Big O notation big-oh of Computational complexity theory	The Big O notation describes the limiting behavior of a function, when the argument tends towards a particular value or infinity.	If f(x) = 6x⁴ − 2x³ + 5 and g(x) = x⁴ , then $f(x)=O(g(x))\mbox{ as }x\to\infty\,$
∞	$\infty \!\,$	infinity infinity numbers	∞ is an element of the extended number line that is greater than all real numbers; it often occurs in limits.	$\lim_{x\to 0} \frac{1}{\|x\|} = \infty$
⌊…⌋	$\lfloor \ldots \rfloor \!\,$	floor floor; greatest integer; entier numbers	⌊x⌋ means the floor of x, i.e. the largest integer less than or equal to x. (This may also be written [x], floor(x) or int(x).)	⌊4⌋ = 4, ⌊2.1⌋ = 2, ⌊2.9⌋ = 2, ⌊−2.6⌋ = −3
⌈…⌉	$\lceil \ldots \rceil \!\,$	ceiling ceiling numbers	⌈x⌉ means the ceiling of x, i.e. the smallest integer greater than or equal to x. (This may also be written ceil(x) or ceiling(x).)	⌈4⌉ = 4, ⌈2.1⌉ = 3, ⌈2.9⌉ = 3, ⌈−2.6⌉ = −2
⌊…⌉	$\lfloor \ldots \rceil \!\,$	nearest integer function nearest integer to numbers	⌊x⌉ means the nearest integer to x. (This may also be written [x], \|\|x\|\|, nint(x) or Round(x).)	⌊2⌉ = 2, ⌊2.6⌉ = 3, ⌊-3.4⌉ = -3, ⌊4.49⌉ = 4
[ : ]	$[\ :\ ] \!\,$	degree of a field extension the degree of field theory	[K : F] means the degree of the extension K : F.	[ℚ(√2) : ℚ] = 2 [ℂ : ℝ] = 2 [ℝ : ℚ] = ∞
[ ] [ , ] [ , , ]	$[\ ] \!\,$ $[\ ,\ ] \!\,$ $[\ ,\ ,\ ] \!\,$	equivalence class the equivalence class of abstract algebra	[a] means the equivalence class of a, i.e. {x : x ~ a}, where ~ is an equivalence relation. [a]_R means the same, but with R as the equivalence relation.	Let a ~ b be true iff a ≡ b (mod 5). Then [2] = {…, −8, −3, 2, 7, …}.
		floor floor; greatest integer; entier numbers	[x] means the floor of x, i.e. the largest integer less than or equal to x. (This may also be written ⌊x⌋, floor(x) or int(x). Not to be confused with the nearest integer function, as described below.)	[3] = 3, [3.5] = 3, [3.99] = 3, [−3.7] = −4
		nearest integer function nearest integer to numbers	[x] means the nearest integer to x. (This may also be written ⌊x⌉, \|\|x\|\|, nint(x) or Round(x). Not to be confused with the floor function, as described above.)	[2] = 2, [2.6] = 3, [-3.4] = -3, [4.49] = 4
		Iverson bracket 1 if true, 0 otherwise propositional logic	[S] maps a true statement S to 1 and a false statement S to 0.	[0=5]=0, [7>0]=1, [2 ∈ {2,3,4}]=1, [5 ∈ {2,3,4}]=0
		image image of … under … everywhere	f[X] means { f(x) : x ∈ X }, the image of the function f under the set X ⊆ dom(f). (This may also be written as f(X) if there is no risk of confusing the image of funder X with the function application f of X. Another notation is Im f, the image off under its domain.)	$\sin [\mathbb{R}] = [-1, 1]$
		closed interval closed interval order theory	$[a,b] = \{x \in \mathbb{R} : a \le x \le b \}$ .	0 and 1/2 are in the interval [0,1].
		commutator the commutator of group theory, ring theory	[g, h] = g⁻¹h⁻¹gh (or ghg⁻¹h⁻¹), if g, h ∈ G (a group). [a, b] = ab − ba, if a, b ∈ R (a ring or commutative algebra).	x^y = x[x, y] (group theory). [AB, C] = A[B, C] + [A, C]B (ring theory).
		triple scalar product the triple scalar product of vector calculus	[a, b, c] = a × b · c, the scalar product of a × b with c.	[a, b, c] = [b, c, a] = [c, a, b].
( ) ( , )	$(\ ) \!\,$ $(\ ,\ ) \!\,$	function application of set theory	f(x) means the value of the function f at the element x.	If f(x) := x², then f(3) = 3² = 9.
		image image of … under … everywhere	f(X) means { f(x) : x ∈ X }, the image of the function f under the set X ⊆ dom(f). (This may also be written as f[X] if there is a risk of confusing the image of funder X with the function application f of X. Another notation is Im f, the image off under its domain.)	$\sin (\mathbb{R}) = [-1, 1]$
		combinations (from) n choose r combinatorics	$\begin{pmatrix} n \\ r \end{pmatrix}$ means the number of combinations of r elements drawn from a set of nelements. (This may also be written as ⁿC_r.)	$\begin{pmatrix} 5 \\ 2 \end{pmatrix} = 10$
		precedence grouping parentheses everywhere	Perform the operations inside the parentheses first.	(8/4)/2 = 2/2 = 1, but 8/(4/2) = 8/2 = 4.
		tuple tuple; n-tuple; ordered pair/triple/etc; row vector; sequence everywhere	An ordered list (or sequence, or horizontal vector, or row vector) of values. (Note that the notation (a,b) is ambiguous: it could be an ordered pair or an open interval. Set theorists and computer scientists often use angle brackets ⟨ ⟩instead of parentheses.)	(a, b) is an ordered pair (or 2-tuple). (a, b, c) is an ordered triple (or 3-tuple). ( ) is the empty tuple (or 0-tuple).
		highest common factor highest common factor; greatest common divisor; hcf; gcd number theory	(a, b) means the highest common factor of a and b. (This may also be written hcf(a, b) or gcd(a, b).)	(3, 7) = 1 (they are coprime); (15, 25) = 5.
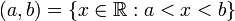( , ) ] , [	$(\ ,\ ) \!\,$ $]\ ,\ [ \!\,$	open interval open interval order theory	$(a,b) = \{x \in \mathbb{R} : a < x < b \}$ . (Note that the notation (a,b) is ambiguous: it could be an ordered pair or an open interval. The notation ]a,b[ can be used instead.)	4 is not in the interval (4, 18). (0, +∞) equals the set of positive real numbers.
(( ))		multichoose multichoose combinatorics	$\textstyle\left(\!\!{n\choose k}\!\!\right)$ means n multichoose x.
( , ] ] , ]	$(\ ,\ ] \!\,$ $]\ ,\ ] \!\,$	left-open interval half-open interval; left-open interval order theory	$(a,b] = \{x \in \mathbb{R} : a < x \le b \}$ .	(−1, 7] and (−∞, −1]
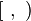[ , ) [ , [	$[\ ,\ ) \!\,$ $[\ ,\ [ \!\,$	right-open interval half-open interval; right-open interval order theory	$[a,b) = \{x \in \mathbb{R} : a \le x < b \}$ .	[4, 18) and [1, +∞)
⟨⟩ ⟨,⟩	$\langle\ \rangle \!\,$ $\langle\ ,\ \rangle \!\,$	inner product inner product of linear algebra	⟨u,v⟩ means the inner product of u and v, where u and v are members of an inner product space. Note that the notation ⟨u, v⟩ may be ambiguous: it could mean the inner product or the linear span. There are many variants of the notation, such as ⟨u \| v⟩ and (u \| v), which are described below. For spatial vectors, the dot product notation, x·y is common. For matrices, the colon notation A : B may be used. As ⟨ and ⟩ can be hard to type, the more “keyboard friendly” forms < and > are sometimes seen. These are avoided in mathematical texts.	The standard inner product between two vectors x = (2, 3) andy = (−1, 5) is: ⟨x, y⟩ = 2 × −1 + 3 × 5 = 13
		average average of statistics	let S be a subset of N for example, 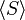$\langle S \rangle$ represents the average of all the element in S.	for a time series :g(t) (t = 1, 2,...) we can define the structure functions S_q( $τ$ ): $S_q = \langle \|g(t + \tau) - g(t)\|^q \rangle_t$
		linear span (linear) span of; linear hull of linear algebra	⟨S⟩ means the span of S ⊆ V. That is, it is the intersection of all subspaces of Vwhich contain S. ⟨u₁, u₂, …⟩is shorthand for ⟨{u₁, u₂, …}⟩. Note that the notation ⟨u, v⟩ may be ambiguous: it could mean the inner productor the linear span. The span of S may also be written as Sp(S).	$\left\lang \left( \begin{smallmatrix} 1 \\ 0 \\ 0 \end{smallmatrix} \right), \left( \begin{smallmatrix} 0 \\ 1 \\ 0 \end{smallmatrix} \right), \left( \begin{smallmatrix} 0 \\ 0 \\ 1 \end{smallmatrix} \right) \right\rang = \mathbb{R}^3$ .
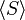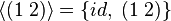		subgroup generated by a set the subgroup generated by group theory	$\langle S \rangle$ means the smallest subgroup of G (where S ⊆ G, a group) containing every element of S. $\langle g_1, g_2, \ldots, \rangle$ is shorthand for $\langle g_1, g_2, \ldots \rangle$ .	In S₃, $\langle(1 \; 2) \rangle = \{id,\; (1 \; 2)\}$ and $\langle (1 \; 2 \; 3) \rangle = \{id, \; (1 \; 2 \; 3),(1 \; 2 \; 3))\}$ .
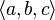		tuple tuple; n-tuple; ordered pair/triple/etc; row vector; sequence everywhere	An ordered list (or sequence, or horizontal vector, or row vector) of values. (The notation (a,b) is often used as well.)	$\langle a, b \rangle$ is an ordered pair (or 2-tuple). $\langle a, b, c \rangle$ is an ordered triple (or 3-tuple). $\langle \rangle$ is the empty tuple (or 0-tuple).
⟨\|⟩ (\|)	$\langle\ \|\ \rangle \!\,$ $(\ \|\ ) \!\,$	inner product inner product of linear algebra	⟨u \| v⟩ means the inner product of u and v, where u and v are members of aninner product space.^[9] (u \| v) means the same. Another variant of the notation is ⟨u, v⟩ which is described above. For spatial vectors, the dot product notation, x·y is common. For matrices, the colon notationA : B may be used. As ⟨ and ⟩ can be hard to type, the more “keyboard friendly” forms < and > are sometimes seen. These are avoided in mathematical texts.
\|⟩	$\|\ \rangle \!\,$	ket vector the ket …; the vector … Dirac notation	\|φ⟩ means the vector with label φ, which is in a Hilbert space.	A qubit's state can be represented as α\|0⟩+ β\|1⟩, where α and βare complex numbers s.t. \|α\|² + \|β\|² = 1.
⟨\|	$\langle\ \| \!\,$	bra vector the bra …; the dual of … Dirac notation	⟨φ\| means the dual of the vector \|φ⟩, a linear functional which maps a ket \|ψ⟩ onto the inner product ⟨φ\|ψ⟩.
∑	$\sum \!\,$	summation sum over … from … to … of arithmetic	$\sum_{k=1}^{n}{a_k}$ means a₁ + a₂ + … + a_n.	$\sum_{k=1}^{4}{k^2}$ = 1² + 2² + 3² + 4² = 1 + 4 + 9 + 16 = 30
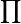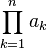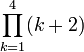∏	$\prod \!\,$	product product over … from … to … of arithmetic	$\prod_{k=1}^na_k$ means a₁a₂···a_n.	$\prod_{k=1}^4(k+2)$ = (1+2)(2+2)(3+2)(4+2) = 3 × 4 × 5 × 6 = 360
∏	$\prod \!\,$	Cartesian product the Cartesian product of; the direct product of set theory	$\prod_{i=0}^{n}{Y_i}$ means the set of all (n+1)-tuples (y₀, …, y_n).	$\prod_{n=1}^{3}{\mathbb{R}} = \mathbb{R}\times\mathbb{R}\times\mathbb{R} = \mathbb{R}^3$
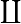∐	$\coprod \!\,$	coproduct coproduct over … from … to … of category theory	A general construction which subsumes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the "least specific" object to which each object in the family admits a morphism.
Δ	$\Delta \!\,$	delta delta; change in calculus	Δx means a (non-infinitesimal) change in x. (If the change becomes infinitesimal, δ and even d are used instead. Not to be confused with the symmetric difference, written ∆, above.)	$\tfrac{\Delta y}{\Delta x}$ is the gradient of a straight line
Δ	$\Delta \!\,$	Laplacian Laplace operator vector calculus	The Laplace operator is a second order differential operator in n-dimensionalEuclidean space	If ƒ is a twice-differentiable real-valued function, then the Laplacian of ƒ is defined by $\Delta f = \nabla^2 f = \nabla \cdot \nabla f$
δ	$\delta \!\,$	Dirac delta function Dirac delta of hyperfunction	$\delta(x) = \begin{cases} \infty, & x = 0 \\ 0, & x \ne 0 \end{cases}$	δ(x)
δ	$\delta \!\,$	Kronecker delta Kronecker delta of hyperfunction	$\delta_{ij} = \begin{cases} 1, & i = j \\ 0, & i \ne j \end{cases}$	δ_ij
∂	$\partial \!\,$	partial derivative partial; d calculus	∂f/∂x_i means the partial derivative of f with respect to x_i, where f is a function on (x₁, …, x_n).	If f(x,y) := x²y, then ∂f/∂x = 2xy
		boundary boundary of topology	∂M means the boundary of M	∂{x : \|\|x\|\| ≤ 2} = {x : \|\|x\|\| = 2}
		degree of a polynomial degree of algebra	∂f means the degree of the polynomial f. (This may also be written deg f.)	∂(x² − 1) = 2
∇	$\nabla \!\,$	gradient del; nabla; gradient of vector calculus	∇f (x₁, …, x_n) is the vector of partial derivatives (∂f / ∂x₁, …, ∂f / ∂x_n).	If f (x,y,z) := 3xy + z², then ∇f = (3y, 3x, 2z)
		divergence del dot; divergence of vector calculus	$\nabla \cdot \vec v = {\partial v_x \over \partial x} + {\partial v_y \over \partial y} + {\partial v_z \over \partial z}$	If $\vec v := 3xy\mathbf{i}+y^2 z\mathbf{j}+5\mathbf{k}$ , then $\nabla \cdot \vec v = 3y + 2yz$ .
		curl curl of vector calculus	$\nabla \times \vec v = \left( {\partial v_z \over \partial y} - {\partial v_y \over \partial z} \right) \mathbf{i}$ $+ \left( {\partial v_x \over \partial z} - {\partial v_z \over \partial x} \right) \mathbf{j} + \left( {\partial v_y \over \partial x} - {\partial v_x \over \partial y} \right) \mathbf{k}$	If $\vec v := 3xy\mathbf{i}+y^2 z\mathbf{j}+5\mathbf{k}$ , then $\nabla\times\vec v = -y^2\mathbf{i} - 3x\mathbf{k}$ .
′	$' \!\,$	derivative … prime; derivative of calculus	f ′(x) means the derivative of the function f at the point x, i.e., the slope of thetangent to f at x. (The single-quote character ' is sometimes used instead, especially in ASCII text.)	If f(x) := x², then f ′(x) = 2x
^•	$\dot{\,} \!\,$	derivative … dot; time derivative of calculus	$\dot{x}$ means the derivative of x with respect to time. That is $\dot{x}(t)=\frac{\partial}{\partial t}x(t)$ .	If x(t) := t², then $\dot{x}(t)=2t$ .
∫	$\int \!\,$	indefinite integral orantiderivative indefinite integral of the antiderivative of calculus	∫ f(x) dx means a function whose derivative is f.	∫x² dx = x³/3 + C
		definite integral integral from … to … of … with respect to calculus	∫_a^b f(x) dx means the signed area between the x-axis and the graph of the functionf between x = a and x = b.	∫_a^b x² dx = b³/3 − a³/3;
		line integral line/ path/ curve/ integral of… along… calculus	∫_C f ds means the integral of f along the curve C, $\textstyle \int_a^b f(\mathbf{r}(t)) \|\mathbf{r}'(t)\|\, dt$ , wherer is a parametrization of C. (If the curve is closed, the symbol ∮ may be used instead, as described below.)
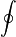∮	$\oint \!\,$	Contour integral; closed line integral contour integral of calculus	Similar to the integral, but used to denote a single integration over a closed curve or loop. It is sometimes used in physics texts involving equations regardingGauss's Law, and while these formulas involve a closed surface integral, the representations describe only the first integration of the volume over the enclosing surface. Instances where the latter requires simultaneous double integration, the symbol ∯ would be more appropriate. A third related symbol is the closed volume integral, denoted by the symbol ∰. The contour integral can also frequently be found with a subscript capital letter C, ∮_C, denoting that a closed loop integral is, in fact, around a contour C, or sometimes dually appropriately, a circle C. In representations of Gauss's Law, a subscript capital S, ∮_S, is used to denote that the integration is over a closed surface.	If C is a Jordan curve about 0, then $\oint_C {1 \over z}\,dz = 2\pi i$ .
π	$\pi \!\,$	projection Projection of relational algebra	$\pi_{a_1, \ldots,a_n}( R )$ restricts $R$ to the $\{a_1,\ldots,a_n\}$ attribute set.	$π Age,Weight (Person)$
π	$\pi \!\,$	Pi pi; 3.1415926; ≈22÷7 mathematical constant	Used in various formulas involving circles; π is equivalent to the amount of area a circle would take up in a square of equal width with an area of 4 square units, roughly 3.14/4. It is also the ratio of the circumference to the diameter of a circle.	A=πR²=314.16→R=10
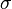σ	$\sigma \!\,$	selection Selection of relational algebra	The selection $σ a θ b (R)$ selects all those tuples in $R$ for which $θ$ holds between the $a$ and the $b$ attribute. The selection $σ a θ v (R)$ selects all those tuples in $R$ for which $θ$ holds between the $a$ attribute and the value $v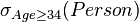$ .	$\sigma_{Age \ge 34}( Person )$ $σ A g e = W e i g h t (P e r s o n)$
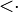<: <·	$<: \!\,$ ${<}{\cdot} \!\,$	cover is covered by order theory	x <• y means that x is covered by y.	{1, 8} <• {1, 3, 8} among the subsets of {1, 2, …, 10} ordered by containment.
<: <·	$<: \!\,$ ${<}{\cdot} \!\,$	subtype is a subtype of type theory	T₁ <: T₂ means that T₁ is a subtype of T₂.	If S <: T and T <: U then S <: U (transitivity).
^†	${}^\dagger \!\,$	conjugate transpose conjugate transpose; adjoint; Hermitian adjoint/conjugate/transpose matrix operations	A^† means the transpose of the complex conjugate of A.^[10] This may also be written A^T, A^T, A^*, A^T or A^T.	If A = (a_ij) then A^† = (a_ji).
^T	${}^{\mathsf{T}} \!\,$	transpose transpose matrix operations	A^T means A, but with its rows swapped for columns. This may also be written A^', A^t or A^tr.	If A = (a_ij) then A^T = (a_ji).
⊤	$\top \!\,$	top element the top element lattice theory	⊤ means the largest element of a lattice.	∀x : x ∨ ⊤ = ⊤
⊤	$\top \!\,$	top type the top type; top type theory	⊤ means the top or universal type; every type in the type system of interest is a subtype of top.	∀ types T, T <: ⊤
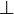⊥	$\bot \!\,$	perpendicular is perpendicular to geometry	x ⊥ y means x is perpendicular to y; or more generally x is orthogonal to y.	If l ⊥ m and m ⊥ n in the plane, then l \|\| n.
		orthogonal complement orthogonal/ perpendicular complement of; perp linear algebra	W^⊥ means the orthogonal complement of W (where W is a subspace of the inner product space V), the set of all vectors in V orthogonal to every vector in W.	Within 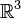$\mathbb{R}^3$ , $(\mathbb{R}^2)^{\perp} \cong \mathbb{R}$ .
		coprime is coprime to number theory	x ⊥ y means x has no factor greater than 1 in common with y.	34 ⊥ 55.
		independent is independent of probability	A ⊥ B means A is an event whose probability is independent of event B.	If A ⊥ B, then P(A\|B) = P(A).
		bottom element the bottom element lattice theory	⊥ means the smallest element of a lattice.	∀x : x ∧ ⊥ = ⊥
		bottom type the bottom type; bot type theory	⊥ means the bottom type (a.k.a. the zero type or empty type); bottom is the subtype of every type in the type system.	∀ types T, ⊥ <: T
		comparability is comparable to order theory	x ⊥ y means that x is comparable to y.	{e, π} ⊥ {1, 2, e, 3, π} under set containment.
⊧	$\vDash \!\,$	entailment entails model theory	A ⊧ B means the sentence A entails the sentence B, that is in every model in which A is true, B is also true.	A ⊧ A ∨ ¬A
⊢	$\vdash \!\,$	inference infers; is derived from propositional logic,predicate logic	x ⊢ y means y is derivable from x.	A → B ⊢ ¬B → ¬A.
⊢	$\vdash \!\,$	partition is a partition of number theory	p ⊢ n means that p is a partition of n.	(4,3,1,1) ⊢ 9, $\sum_{\lambda \vdash n} (f_\lambda)^2 = n!$ .
o	$\circ \!\,$	Hadamard product entrywise product linear algebra	For two matrices (or vectors) of the same dimensions $A, B \in {\mathbb R}^{m \times n}$ the Hadamard product is a matrix of the same dimensions $A \circ B \in {\mathbb R}^{m \times n}$ with elements given by $(A \circ B)_{i,j} = (A)_{i,j} \cdot (B)_{i,j}$ . This is often used in matrix based programming such as MATLAB where the operation is done by A.*B	$\begin{bmatrix} 1&2 \\ 2&4 \\ \end{bmatrix} \circ \begin{bmatrix} 1&2 \\ 0&0 \\ \end{bmatrix} = \begin{bmatrix} 1&4 \\ 0&0 \\ \end{bmatrix}$

CREDITS: http://en.wikipedia.org/wiki/List_of_mathematical_symbols

Click click CLICKS

Formulae

No comments:

Post a Comment